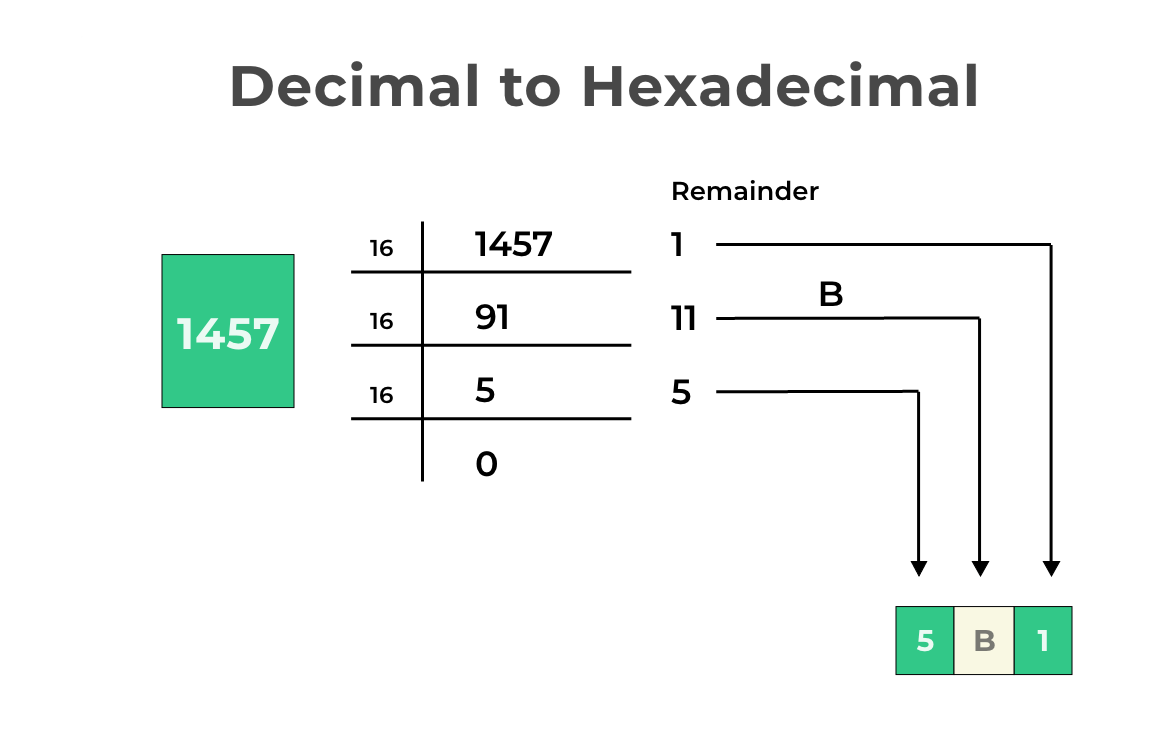
Converting hexadecimal numbers like 0x2F to decimal is an essential skill for programmers, engineers, and anyone working with computer systems. Whether you're coding, analyzing data, or simply curious about how computers process information, understanding hexadecimal-to-decimal conversion is crucial. This article will provide you with a complete guide to understanding the process of converting 0x2F to decimal.
Hexadecimal numbers, often referred to as "hex," are widely used in computing due to their compact representation of binary data. They are particularly useful in programming languages, memory addresses, and color codes in web design. By the end of this article, you'll not only know how to convert 0x2F to decimal but also gain a deeper understanding of the underlying principles.
We'll explore the fundamental concepts behind hexadecimal and decimal systems, walk through step-by-step conversion processes, and provide practical examples to reinforce your learning. Let's dive in!
Read also:Kings Head British Pub A True Taste Of Britain
Table of Contents
- What is Hexadecimal?
- Hexadecimal to Decimal Basics
- The Conversion Process
- Step-by-Step Example: Converting 0x2F to Decimal
- Common Use Cases for Hexadecimal Numbers
- Tools and Calculators for Hexadecimal Conversion
- Advanced Techniques in Hexadecimal Conversion
- Hexadecimal in Computer Programming
- Troubleshooting Common Conversion Errors
- Conclusion
What is Hexadecimal?
Hexadecimal is a base-16 numeral system that uses sixteen distinct symbols for representation. These symbols include the numbers 0 through 9 and the letters A through F, where A represents 10, B represents 11, and so on up to F, which represents 15. Hexadecimal is widely used in computing because it provides a more human-readable representation of binary data.
The hexadecimal system is particularly advantageous in scenarios where large binary numbers need to be expressed concisely. For instance, a single hexadecimal digit can represent four binary digits (bits), making it easier to work with memory addresses, color codes, and other binary-related data.
Hexadecimal to Decimal Basics
Before diving into the conversion process, it's important to understand the relationship between hexadecimal and decimal systems. Decimal, or base-10, is the numeral system most people are familiar with, using the digits 0 through 9. Hexadecimal, on the other hand, extends this range to include letters A through F.
Each position in a hexadecimal number represents a power of 16, just as each position in a decimal number represents a power of 10. This positional notation is the foundation for converting between the two systems.
The Conversion Process
Understanding Positional Notation
Positional notation is the key to converting hexadecimal numbers to decimal. In this system, each digit in a number is multiplied by the base raised to the power of its position. For example, in the hexadecimal number 0x2F:
- The rightmost digit (F) represents \(15 \times 16^0\).
- The leftmost digit (2) represents \(2 \times 16^1\).
By summing these values, you can calculate the decimal equivalent of the hexadecimal number.
Read also:Big Barry The Untold Story Of A Remarkable Personality
Step-by-Step Example: Converting 0x2F to Decimal
Let's break down the conversion process for the hexadecimal number 0x2F:
- Identify the digits: 2 and F.
- Assign their decimal equivalents: 2 remains 2, and F is 15.
- Multiply each digit by \(16^n\), where \(n\) is the position of the digit (starting from 0 on the right).
- Sum the results: \(2 \times 16^1 + 15 \times 16^0 = 32 + 15 = 47\).
Therefore, 0x2F in hexadecimal is equivalent to 47 in decimal.
Common Use Cases for Hexadecimal Numbers
Hexadecimal in Memory Addresses
Hexadecimal is frequently used to represent memory addresses in computer systems. This is because memory addresses are often 32 or 64 bits long, and expressing them in hexadecimal makes them more manageable. For example, the address 0x7FFF1234 is much easier to read than its binary equivalent.
Hexadecimal in Color Codes
In web design, hexadecimal is used to define colors using the RGB (Red, Green, Blue) model. Each color component is represented by two hexadecimal digits, resulting in a six-character code. For instance, the color white is represented as #FFFFFF, while black is #000000.
Tools and Calculators for Hexadecimal Conversion
While manual conversion is a valuable skill, there are numerous tools and calculators available to simplify the process. Websites like RapidTables and EasyCalculation offer free hexadecimal-to-decimal converters. Additionally, most programming languages provide built-in functions for performing these conversions.
Advanced Techniques in Hexadecimal Conversion
Using Binary as an Intermediate Step
Another method for converting hexadecimal to decimal involves using binary as an intermediate step. Each hexadecimal digit can be converted to its four-bit binary equivalent, and the resulting binary number can then be converted to decimal. This method is particularly useful for understanding the underlying binary representation of hexadecimal numbers.
Hexadecimal in Computer Programming
Hexadecimal numbers are integral to many programming languages, especially those that involve low-level operations or direct memory manipulation. For example, in C and C++, hexadecimal constants are prefixed with 0x, making it easy to identify and work with them in code.
Troubleshooting Common Conversion Errors
When converting hexadecimal numbers to decimal, common errors include misinterpreting the positional values or mistyping the digits. To avoid these mistakes:
- Double-check the hexadecimal digits and their corresponding decimal values.
- Verify the positional powers of 16.
- Use a calculator or tool to cross-check your results.
Conclusion
Converting hexadecimal numbers like 0x2F to decimal is a fundamental skill with numerous applications in computing and programming. By understanding the principles of positional notation and practicing step-by-step conversion techniques, you can master this process and apply it effectively in various scenarios.
We encourage you to practice converting other hexadecimal numbers to decimal and explore the resources mentioned in this article. If you found this guide helpful, please share it with others or leave a comment below. Additionally, feel free to explore our other articles for more in-depth knowledge on related topics.
References:
- Wikipedia - Hexadecimal
- RapidTables - Hex to Decimal Converter
- GeeksforGeeks - Hexadecimal to Decimal Conversion